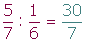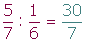Concepto de fracción
4/5
5 denominador , indica el número de partes en que se ha dividido la unidad.4 numerador , indica el número de unidades fraccionarias elegidas.
Representación de fracciones
Clases de fracciones
Fracciones propias
Las fracciones propias son aquellas cuyo numerador es menor que el denominador. Su valor está comprendido entre cero y uno.
Ejemplo:
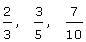
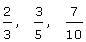
Fracciones impropias
Las fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Su valor es mayor que 1.Ejemplo:
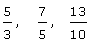
Fracciones decimales
Ejemplo:
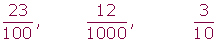
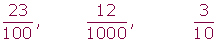
Fracciones equivalentes
Dos fracciones son equivalentes cuando tienen el mismo valor decimal. Las fracciones equivalentes representan la misma parte de una unidad o entero.
Ejemplo:
 Si lo representamos tenemos :
Si lo representamos tenemos :

¿Por qué son lo mismo? Porque cuando multiplicas o divides a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es:

2- Amplificación de fracciones
Amplificar una fracción consiste en encontrar una fracción equivalente pero con sus términos (numerador y denominador) mayores.
Para amplificar una fracción basta con multiplicar el numerador y el denominador por el mismo número
Ejemplo :
 Luego las fracciones 3 y 18 son equivalentes.
Luego las fracciones 3 y 18 son equivalentes.
5 30
3- Simplificar una fracción
Simplificar una fracción consiste en encontrar una fracción equivalente pero con sus términos(numerador y denominador) más pequeños.
Para simplificar una fracción debe existir un número entre el que podamos dividir el numerador y el denominador de manera exacta.
Es decir, para poder simplificar una fracción el numerador y el denominador tienen que tener algún divisor común (no pueden ser primos entre sí)
Ejemplos de los dos casos:

 Las fracciones que no se pueden simplificar más se les llama irreducibles, esto sucede cuando el numerador y el denominador son primos entre sí.
Las fracciones que no se pueden simplificar más se les llama irreducibles, esto sucede cuando el numerador y el denominador son primos entre sí.
- Aunque se puede empezar a simplificar dividiendo por cualquier número, se debe seguir un orden lógico (por ejemplo los primos: 2, 3, 5, ..), es decir, probamos dividir ambos entre 2 mientras se pueda, después pasamos al 3 y así sucesivamente.
Simplificar una fracción es transformarla en una fracción equivalente más simple.
1 Para simplificar una fracción dividimos numerador y denominador por un mismo número.
2 Empezaremos a simplificar probando por los primeros números primos: 2, 3, 5, 7, ... Es decir, probamos a dividir numerador y denominador entre 2 mientras se pueda, después pasamos al 3 y así sucesivamente.
3 Se repite el proceso hasta que no haya más divisores comunes.
4 Si los términos de la fracción terminan en ceros, empezaremos quitando los ceros comunes finales del numerador y denominador, lo cual es equivalente a dividir numerador y denominador por la misma potencia de 10.
5 Si el número por el que dividimos es el máximo común divisor del numerador y denominador llegamos a una fracción irreducible.
Ejemplo:
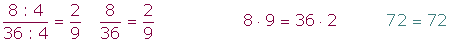
Las fracciones irreducibles son aquellas que no se pueden simplificar, esto sucede cuando el numerador y el denominador son primos entre sí, o lo que es lo mismo, cuando el mcd de ambos números es 1.
Ejemplo:
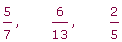
Reducir varias fracciones a común denominador consiste en convertirlas en otras equivalentes que tengan el mismo denominador. Para ello:
1 Se determina el denominador común, que será el mínimo común múltiplo de los denominadores.
2 Este denominador común se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
Ejemplo:
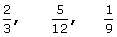
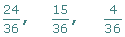
De dos fracciones que tienen el mismo numerador es menor el que tiene mayor denominador.
En primer lugar las tenemos que poner a común denominador.
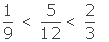
En primer lugar se reducen los denominadores a común denominador calculando su mcm, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.
Ejemplo:
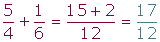
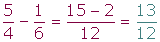
La multiplicación de dos fracciones es otra fracción que tiene:
1Por numerador el producto de numeradores.
2 Por denominador el producto de denominadores.
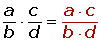
La división de dos fracciones es otra fracción que tiene:
1 Por numerador el producto de los extremos.
2 Por denominador el producto de los medios.
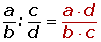
Ejemplo:

¿Por qué son lo mismo? Porque cuando multiplicas o divides a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es:
¡Lo que haces a la parte de arriba de la fracción también lo tienes que hacer a la parte de abajo!

Para saber si dos fracciones son equivalente podemos multiplicar en cruz, es decir el numerador de la primera fracción por el denominador de la segunda y el numerador de la segunda por el denominador de la primera y ambas multiplicaciones han de dar lo mismo.
2- Amplificación de fracciones
Amplificar una fracción consiste en encontrar una fracción equivalente pero con sus términos (numerador y denominador) mayores.
Para amplificar una fracción basta con multiplicar el numerador y el denominador por el mismo número
Ejemplo :

5 30
3- Simplificar una fracción
Simplificar una fracción consiste en encontrar una fracción equivalente pero con sus términos(numerador y denominador) más pequeños.
Para simplificar una fracción debe existir un número entre el que podamos dividir el numerador y el denominador de manera exacta.
Es decir, para poder simplificar una fracción el numerador y el denominador tienen que tener algún divisor común (no pueden ser primos entre sí)
Ejemplos de los dos casos:


- Aunque se puede empezar a simplificar dividiendo por cualquier número, se debe seguir un orden lógico (por ejemplo los primos: 2, 3, 5, ..), es decir, probamos dividir ambos entre 2 mientras se pueda, después pasamos al 3 y así sucesivamente.
Simplificar fracciones
1 Para simplificar una fracción dividimos numerador y denominador por un mismo número.
2 Empezaremos a simplificar probando por los primeros números primos: 2, 3, 5, 7, ... Es decir, probamos a dividir numerador y denominador entre 2 mientras se pueda, después pasamos al 3 y así sucesivamente.
3 Se repite el proceso hasta que no haya más divisores comunes.
4 Si los términos de la fracción terminan en ceros, empezaremos quitando los ceros comunes finales del numerador y denominador, lo cual es equivalente a dividir numerador y denominador por la misma potencia de 10.
5 Si el número por el que dividimos es el máximo común divisor del numerador y denominador llegamos a una fracción irreducible.
Ejemplo:
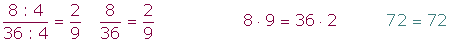
Fracciones irreducibles
Ejemplo:
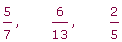
1 Se determina el denominador común, que será el mínimo común múltiplo de los denominadores.
2 Este denominador común se divide por cada uno de los denominadores, multiplicándose el cociente obtenido por el numerador correspondiente.
Ejemplo:
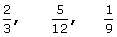
12 = 22 · 3
9 = 32 · 3
m.c.m.(3. 12. 9) = 22 · 32 = 36
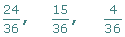
1 Ordenar fracciones con igual denominador
De dos fracciones que tienen el mismo denominador es menor la que tiene menor numerador.
Ejemplo:
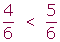
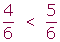
2 Ordenar fracciones con igual numerador
Ejemplo:
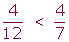
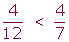
3 Ordenar fracciones con numeradores y denominadores distintos
Ejemplo:
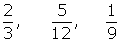
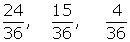
Es menor la que tiene menor numerador.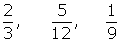
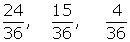
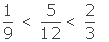
Suma y resta de fracciones con distinto denominador
Ejemplo:
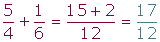
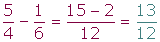
Multiplicación de fracciones
1Por numerador el producto de numeradores.
2 Por denominador el producto de denominadores.
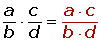
Ejemplo: 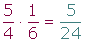
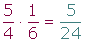
División de fracciones
1 Por numerador el producto de los extremos.
2 Por denominador el producto de los medios.
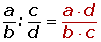
Ejemplo: