NÚMEROS DECIMALES

1- Lectura y escritura de números decimales.

2- Comparación de números decimales.

3- Números decimales y  fracciones decimales.
4- Números decimales comprendidos entre dos números decimales.

5- Suma y resta de números decimales.

6- Multiplicación de números decimales.

7- Aproximación y estimación de números decimales. Truncamiento.

8- División de números decimales.
9- Porcentajes

10- Problemas

1- Lectura y escritura de números decimales.

Un nº decimal consta de:

• Una parte entera a la izquierda de la coma.
• Parte decimal a la derecha de la coma.

Para leer números decimales, seguimos el siguiente esquema:

Primero leemos la parte entera del nº y decimos a continuación unidades o enteros y después pasamos a leer la parte decimal colocando al final el nombre del lugar que ocupa la última cifra.

eje. 3,098- tres unidades o enteros y noventa y ocho milésimas.

2- Comparación de números decimales.

De dos números decimales es mayor el que tenga mayor parte entera.Si ambas son iguales es mayor el que tenga mayor la cifra de las décimas, si siguen siendo iguales, el que tenga mayor la cifra de las centésimas, etc
 

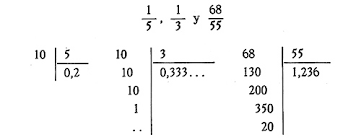
3- Números decimales y fracciones decimales.

Decimos que una fracción es decimal cuando su denominador es la unidad seguida de ceros. 

Para transformar un nº decimal en fracción decimal, se coloca como numerador de la fracción el nº sin coma y como denominador la unidad seguida de tantos ceros como cifras decimales tenía el nº.De igual modo podemos transformar una fracción decimal en un nº decimal.

Ejemplo:

4,235= 4235/1000

25/1000= 0,025

  

4- Números decimales comprendidos entre dos números decimales.

El conjunto de los números decimales es un conjunto denso, porque entre dos números decimales siempre hay otro nº decimal.

Eje. Escribe un número decimal comprendido entre 3,4 y 3,5......3,4<  3,41< 3,5     Entre 3,41< 3,42<3,5           3,42<3,43<3,5

5- Suma y resta de números decimales.

 Para sumar o restar números decimales:

• Se escriben uno debajo del otro con las comas alineadas.
• Se suman o se restan como si fueran números naturales.
• Al resultado se le coloca la coma alineada. 
•  

6- Multiplicación de números decimales.

Para multiplicar números decimales:

• Se multiplican los números sin tener en cuenta la coma.
• En el resultado se separan con la coma tantas cifras decimales como tengan entre los dos.

Para multiplicar por 0,1; 0,01; 0,001....se desplaza la coma a la izquierda tantas posiciones como ceros hay delante del 1

Para multiplicar por 10, 100, 1000,....se desplaza la coma a la derecha tantas posiciones como ceros hay detrás del 1
 

7-  Aproximación y estimación de números decimales.

Los números decimales los podemos redondear a la unidad, a la décima o a la centésima.
a) Redondear a la unidad
Redondear a la unidad implica sustituirlo por el número que más se le aproxime sin decimales.

Si la parte decimal es igual o inferior a 0,500 se redondea a la unidad inferior; si es mayor que 0,500 se redondea a la unidad superior.

Veamos algunos ejemplos:
43,5

Este número se sitúa entre 43 y 44. Hay que ver a cual de ellos se redondea.
La parte decimal es 0,5 (como no tiene centésimas ni milésimas equivale a 0,500). Al ser esta parte decimal igual o inferior a 0,500 redondeamos a la unidad inferior.
Por lo tanto 43,5 lo redondeamos a 43.

27,31

Este número se sitúa entre 27 y 28.
La parte decimal es 0,31 (como no tiene milésimas equivale a 0,310). Al ser esta parte decimal inferior a 0,500 redondeamos a la unidad inferior.
Por lo tanto 27,31 lo redondeamos a 27.

58,721

Este número se sitúa entre 58 y 59.
La parte decimal es 0,721. Al ser esta parte decimal superior a 0,500 redondeamos a la unidad superior.
Por lo tanto 58,721 lo redondeamos a 59.

b) Redondear a la décima
Redondear un número a la décima implica sustituirlo por el número que más se le aproxime y que en la parte decimal tan sólo tenga décimas.

Si la parte centesimal es igual o inferior a 0,050 se redondea a la décima inferior; si es mayor que 0,050 se redondea a la décima superior.

Veamos algunos ejemplos:
22,53

Este número se sitúa entre 22,5 y 22,6.
La parte centesimal es 0,03 (como no tiene milésimas equivale a 0,030). Al ser esta parte centesimal inferior a 0,050 redondeamos a la décima inferior.
Por lo tanto 22,53 lo redondeamos a 22,5.

62,27

Este número se sitúa entre 62,2 y 62,3.
La parte centesimal es 0,07 (como no tiene milésimas equivale a 0,070). Al ser esta parte centesimal superior a 0,050 redondeamos a la décima superior.
Por lo tanto 62,27 lo redondeamos a 62,3.

84,662

Este número se sitúa entre 84,6 y 84,7.
La parte centesimal es 0,062. Al ser esta parte centesimal superior a 0,050 redondeamos a la décima superior.
Por lo tanto 84,662 lo redondeamos a 84,7.

c) Redondear a la centésima
Redondear un número a la centésima implica sustituirlo por el número que más se le aproxime y que en la parte decimal tenga hasta centésimas.

Si la parte milesimal es igual o inferior a 0,005 se redondea a la centésima inferior; si es mayor que 0,005 se redondea a la centésima superior.

Veamos algunos ejemplos:
17,124

Este número se sitúa entre 17,12 y 17,13.
La parte milesimal es 0,004. Al ser esta parte milesimal inferior a 0,005 redondeamos a la centésima inferior.
Por lo tanto 17,124 lo redondeamos a 17,12.

26,33

Este número se sitúa entre 26,33 y 26,34.
La parte milesimal es 0,000. Al ser esta parte milesimal inferior a 0,005 redondeamos a la centésima inferior.
Por lo tanto 26,33 lo redondeamos a 26,33.

77,258

Este número se sitúa entre 77,25 y 77,26.
La parte milesimal es 0,008. Al ser esta parte milesimal superior a 0,005 redondeamos a la centésima superior.
Por lo tanto 77,258 lo redondeamos a 77,26.

Truncamiento de un nº decimal.

En el truncamiento de un número decimal se eliminan las cifras a partir de aquellas en la que se realiza el truncamiento.
- Truncamiento por la unidad: se eliminan todas las cifras decimales.

45,325 se trunca por 45
122,3434 se trunca por 122
91,435123 se trunca por 91

- Truncamiento por la décima: tan sólo se deja esta cifra decimal:

45,325 se trunca por 45,3
122,3434 se trunca por 122,3
91,435123 se trunca por 91,4

- Truncamiento por la centésima: tan sólo se dejan dos cifras decimales:

45,325 se trunca por 45,32
122,3434 se trunca por 122,34
91,435123 se trunca por 91,43

8- División de números decimales. 

1. Dividir un nº decimal entre un nº natural.

Se hace la división como si fueran dos números naturales, pero al bajar la cifra de las décimas se pone la coma en el cociente.

526.6562 : 7 = 75.2366

    2. Dividir un nº natural entre un nº decimal.

Se multiplica el divisor por la unidad seguida de tantos ceros como cifras decimales tenga el nº convirtiéndose así en un nº natural. A continuación se multiplica el dividendo por el mismo nº, quedando así ambos compensados por la ley fundamental de la división. 

 5126 : 62.37 = 82.18

 

3. Dividir dos números decimales.

Se multiplica el divisor por la unidad seguida de tantos ceros como cifras decimales tenga el nº convirtiéndose así en un número natural. A continuación se multiplica el dividendo por el mismo nº, quedando así ambos compensados por la ley fundamental de la división.De esta forma el dividiendo puede quedar como número natural o bien como número decimal. Si el dividendo quedara como decimal procederemos como el el punto uno de este apartado.

5627.64 : 67.5261 = 83.34



9- Porcentajes 
Un porcentaje es una fracción que tiene por denominador100. Nos dice que parte de un total representa una cantidad. Para calcular el porcentaje de una cantidad multiplicamos esa cantidad por el nº del porcentaje y la dividimos entre 100.

También podemos considerar el porcentaje como una multiplicación por un nº decimal, para ello procedemos del siguiente modo:
30%= 30/100= 0,30


 Ejemplo:
Calcula el 20% de 1200
1200X20= 24000; 24000: 100= 240.

También podemos calcularlo del siguiente modo:
20% de  1200= 20/100 de 1200= 0,20 X 1200= 240.

10- Problemas

1-Una jarra vacía pesa 0.64 kg, y llena de agua 1.728 kg. ¿Cuánto pesa el agua?

2-Un ciclista ha recorrido 145.8 km en una etapa, 136.65 km en otra etapa y 162.62 km en una tercera etapa. ¿Cuántos kilómetros le quedan por recorrer si la carrera es de 1000 km?

3- De un depósito con agua se sacan 184.5 l y después 128.75 l, finalmente se sacan 84.5 l. Al final quedan en el depósito 160 l. ¿Qué cantidad de agua había el depósito?

4- Se tienen 240 cajas con 25 bolsas de café cada una. Si cada bolsa pesa 0.62 kg, ¿cuál es el peso del café?

5-Sabiendo que 2.077 m³ de aire pesan 2.7 kg, calcular lo que pesa 1 m³ de aire.

6-Eva sigue un régimen de adelgazamiento y no puede pasar en cada comida de 600 calorías.
Ayer almorzó : 125 g de pan, 140 g de espárragos, 45 g de queso y una manzana de 130 g.
Si 1 g de pan da 3.3 calorías, 1 g de espárragos 0.32, 1 g de queso 1.2 y 1 g de manzana 0.52.


Problemas de porcentajes.

1- El prensado de 1.500 kg de aceituna produjo el 36%
de su peso en aceite. Calcula la cantidad de aceite
obtenida.
2- Si hoy han faltado a clase  por enfermedad el 20%
de los 30 alumnos/as, ¿cuántos alumnos han asistido?
¿Cuántos alumnos/as han faltado?
3- Los embalses de agua que abastecen a una ciudad
tienen  una  capacidad  total  de  400  km³ ,  y  se
encuentran al 27 % de su capacidad. ¿Cuantos km³
contienen?
4-

¿Respetó Eva su régimen?